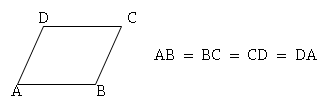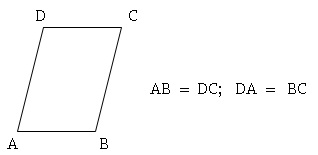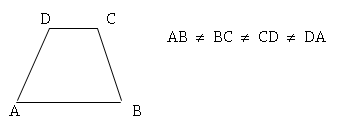¿Qué son los
cuadriláteros?
Los
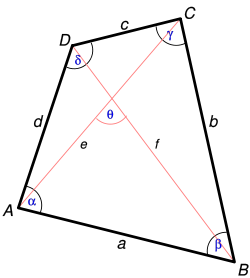
cuadriláteros son figuras geométricas que tienen cuatro lados y cuatro
ángulos.
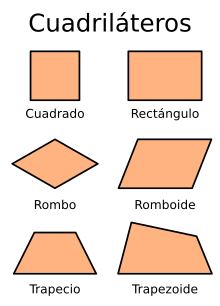
Se clasifican
en:
Paralelógramos
Trapecios
Trapezoides
Paralelógramos: Cuadrilátero que tiene dos pares de lados
paralelos. Los paralelogramos son: el cuadradro,
rectángulo, rombo y romboide.
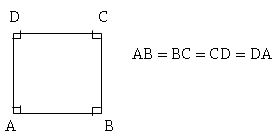
a) Cuadrado: Todos sus lados son de igual medida.
Todos sus ángulos miden 90º.
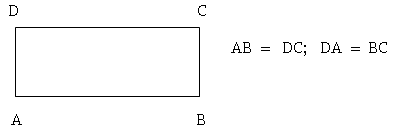
b) Rectángulo: Tiene dos pares de igual
medida. Todos sus ángulos son rectos.
c) Rombo: Todos sus lados son de igual medida.
Sus ángulos no son rectos; dos son agudos y dos son obtusos (los ángulos
opuestos).
d) Romboide: Tiene dos pares de lados de igual
medida. Dos pares de sus ángulos son agudos y dos pares son obtusos
Trapecios: Son
cuadriláteros que tiene solamente un par de lados paralelos. Los
trapecios son: trapecio isósceles, trapecio rectángulo, trapecio trisolátero y trapecio escaleno.
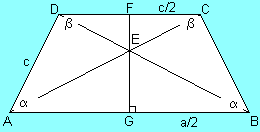
Trapecio
isósceles: tiene un par de lados paralelos de igual medida.
Sus ángulos basales son iguales
AD = BC
< DAB = < ABC
e no es perpendicular con f
e = f
Las diagonales no son bisectrices.
α + β = 180 º
AE = EB, ED = EC, EG = 2EF
El trazo FG (perpendicular a las bases divide a cada base en la
mitad)
|
|
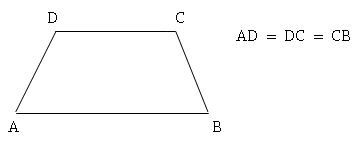
Trapecio trisolátero: Es el que tiene tres lados de igual
medida. Sus ángulos basales son de igual medida, respectivamente.
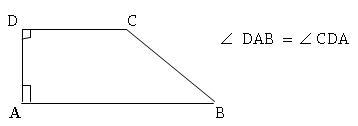
a) Trapecio
rectángulo: Es el que tiene dos ángulos rectos, es decir, un ángulo
de 90º.
b) Trapecio
escaleno: Tiene todos sus lados de distinta medida. Sus ángulos basales también son diferentes.
Trapezoides: Son< aquellos cuadriláteros
que no tienen lados paralelos. Ellos son el trapezoide simétrico y
el trapezoide asimétrico.
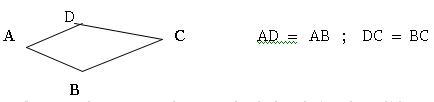
a) trapezoide simétrico: Tiene dos
pares de lados de igual medida.
b) Trapezoide asimétrico: Puede tener
dos lados de igual medida, tres lados de igual medida o bien ninguno.
Ver, en
Internet: